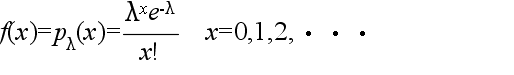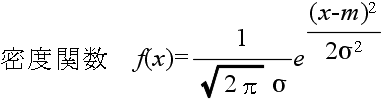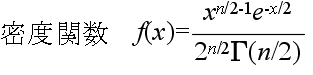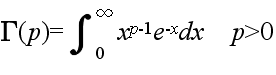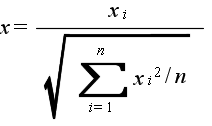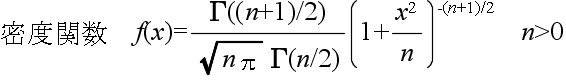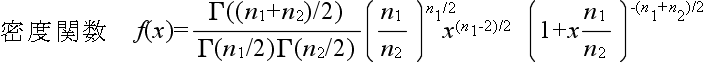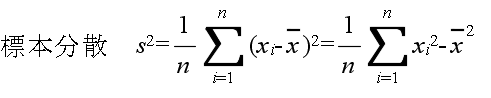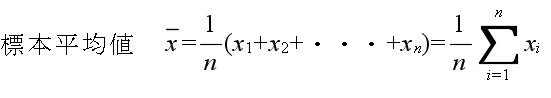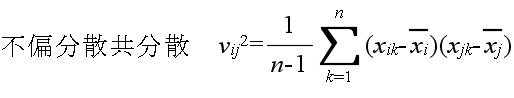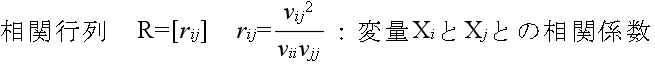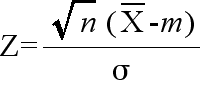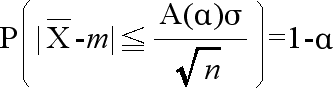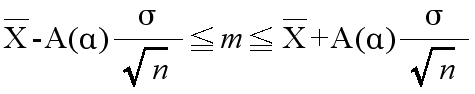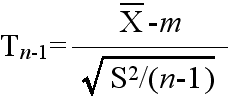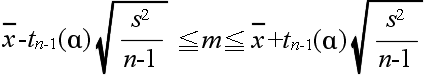男の麻雀ポリシー > 【139】『参考資料・01 男の麻雀に必要な確率・統計の知識』
| 『参考資料・01 男の麻雀に必要な確率・統計の知識』 |
| ・確率統計の計算が必要になった場合の備忘録。 |
http://www.sist.ac.jp/~suganuma/kougi/other_lecture/SE/math/prob/prob.htm#1
http://dora12.net/modules/university/stat/toukei/ka1.html









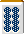




西は役牌ではありません。何を切るのが最も和了率が高いでしょう?
先日フォーラムで上がった議題です。
ある程度うまくなってくれば両面ターツを一つ落とすのが早いというのは知っている人が多いと思います。
では本当にそうか?これを計算してみます。
A:縦フォロー落とし(ターツオーバーに受ける)
B:両面落とし
と置きます。
*Aには「一向になったあと完全形になる」
Bには「二向時で一向時の完全形を確定させる」
それぞれ縦引きの手変わりがありますが、
片方が一方的に有利となる情報ではないためとりあえず無視します。
まずここで
A 二向受け32枚 一向受け16枚より
32/134×16/134
B 二向受け16枚からは一向受け20枚
二向受け12枚からは一向受け16枚より
16/134×20/134 + 12/134×16/134
これが512/134^2で一致するため、
スピードは同等なのではないか?
この考え方に触れておきましょう。
よく見る計算方なのでこれを念頭に置いて以下の文を読むと理解が深まると思います。
確かに確率の掛け算になっているし妥当なようにも見えますが、
実はこれは誤りです。
厳密に確率計算をする場合、
成功率×成功率
の計算ではいけません。
なぜなら成功率というのは1巡あたりの成功率であるからで、
これだとあと2順で聴牌する確率になっています。
ちなみに2巡でのテンパイ率ならこの計算通り一致します。
かといってこれを○巡目まで出していくといつかは聴牌するわけですから、
どんな受けでも計算結果は100%になってしまいます。
でどうするかと言うと、スピードをみるわけです。
今回の事象の「失敗」は他家の和了や聴牌、流局等、
巡目によって増えていく危険のみによって生まれます。
つまり早ければ早いほど成功率は上がる訳です。
よってシャンテン成功率は消費巡目と単調相関しますから、
シャンテン成功率は「成功までの平均消費巡目」で評価できることになります。
でこれを計算すると、
確率pの事象が1回成功するまでにかかる試行回数の平均は
Σ p(k+1)(1-p)^k
等比数列の和で簡単に分解でき結果は1/p
今回は2つの事象が成功するまでの試行回数で、それぞれは独立だから
一向の成功率をp、二向の成功率をqとおくと
1/p+1/q が成功率を評価する式になります。
今回の場合をみると
A(二向を強く)
134/32+134/16
B(一向を強く)
134/28+(16×134/20+12×134/16)/(16+12)
{後者は16枚からの134/20と12枚からの134/16の平均値}
計算すると12.56 vs 12.2
でBの一向強化が強いことがわかります。
これほど良形同士の比較でも1/3順も違うのは大きいですね。
ちなみにわざわざ計算しなくともこの手の問題は一般化できます。
受けの枚数を同等とすると、
p+q=k (kは定数) とおけ、
このとき成功率の評価式Xは
X=1/p+1/q
=1/p+1/(k-p)
=k/p(k-p)
p(k-p)はご存知上に凸となる二次関数ですから、
p=k/2で最大値を取り、両側に単調減少していきます。
p=k/2ならばp=q
よってpとqの差が小さいほどXは小さく、つまり早く張れることになり
受けの枚数の総和が等しいとき、
一向聴と二向聴の受けの枚数の差が小さいほど聴牌率は上がる
が導けます。
「確率の小さい方を助けましょう」というのはここからきていますね。
これがわかっていれば上記の計算は必要ありません。
一般的に一向聴の受けを最大にせよというのはこの式によって証明できます。
- 1.順列・組合せ
- 1.1 順列・組合せ
| [定義] 有限個の対象から幾つかを取り出しそれを順に並べたものを順列という.一方,取り出した順序を問題にしないで,それらの組合せだけに注目するとき,その組を組合せという. |
- 例1: 例えば,3 個の数字 {1, 2, 3} から,2 個の数字を取り出した順列は,
- (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2)
- の 6 種類あります.しかし,組み合わせは,順序を問題にしませんので,
- (1, 2), (1, 3), (2, 3)
- の 3 種類になります.
- [定理] 相異なる n 個のものから r 個をとる順列の総数は,
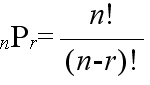
- である.
|
- [定理] n 個のものから r 個を取り出す組合せの数は,
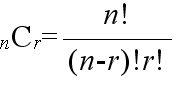
- である.
|
- 例1の場合に対して,上記の定理を使用して順列及び組み合わせの数を計算すれば,6 及び 3 になることは明らかだと思います.
以下,特別な場合に対する,順列や組み合わせの数を計算するための定理をあげておきます.
n 個の中の p 個が同じものであれば,nPn の中には,p 個の並べ方( p! )だけ同じ順列が含まれています.このことを考慮すれば,以下の定理は明らかだと思います.
- [定理] n 個の内で,p 個は同じもの,q 個は他の同じもの,・・・,s 個がまた他の同じものであるとき,これらの
n 個を並べる順列の数は,
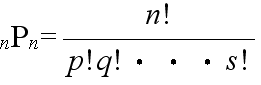
- である.
|
- [定理] 相異なる n 個のものを円形に並べる順列(円順列)の数は,
- n-1Pn-1 = (n - 1)!
- である.
|
- [定理] n 個のものから重複を許して r 個とる順列(重複順列)の数は,
- nΠr = nr
- である.
|
- [定理] n 個の中から,重複を許して r 個とる組合せの数は,
- nHr = n+r-1Cr
- である( r < n とは限らない)
|
- [定理] 組合せの数 nCr に関しては,次の式が成り立つ
- nCr = nCn-r
- nCr = n-1Cr + n-1Cr-1 (パスカルの公式)
|
- 1.2 二項定理
- [定理] 二項定理
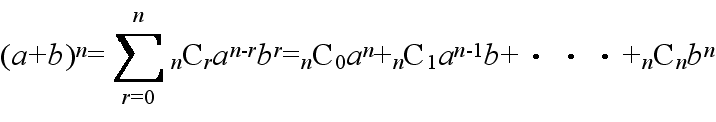
|
- nCr のことを二項係数と呼び,
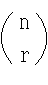
- のようにも記述します.
|
- 例えば,この定理を利用することによって,
- (x + 2)10
- における x7の係数を,
- 10C327 = 120 x 128 = 15360
- のようにして,計算することができます.また,下の定理は,二項定理の拡張です.
- [定理] 多項定理
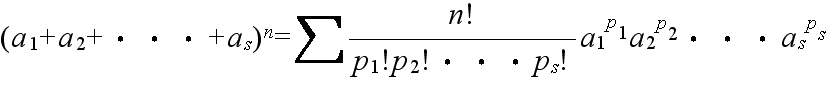
- ただし,p1, p2, ・・・, ps は 0 または正の整数であり,Σ は p1 + p2 + ・・・ + ps = n となるすべての整数値 p1, p2, ・・・, ps についての和を表す.
|
- ここで,
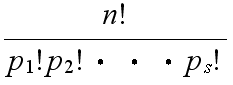
- を多項係数と呼び,以下のようにも記述されます.
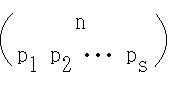
|
- 2.確率
- 2.1 事象
| [定義] 一定の条件の下で繰り返し行うことができ,その結果が偶然に支配されるような実験や観測を一般に試行という.試行によって起こる可能性のあるすべての事柄の集合 Ω が確定しているとき,その集合を考えている試行の標本空間といい,その要素を標本点,または,単に標本空間の点という. |
- [定義] 標本空間 Ω の部分集合を事象といい,試行の結果が1つの事象Aに属するとき,事象Aが起こったという.標本点の1つ1つを特に根元事象という.それに対して,2個以上の点からなる事象を複合事象という.また,標本空間全体を全事象,決して起こらない事柄は空集合 φ で表され,それを空事象という.
|
- 例1: 1つのさいころを,1回だけ投げることについて考えてみます.明らかに,この結果は偶然性に左右され,試行と考えることができます.このとき,標本空間
Ω は,「k の目が出る」ことを k で表すと,
- Ω = {1, 2, 3, 4, 5, 6}
- となります.根元事象は,1, 2, 3, 4, 5, 及び, 6 であり,また,複合事象としては,いろいろ考えられますが,「偶数の目が出る事象A」という場合であれば,以下のようになります.
- 偶の目が出る事象A = {2, 4, 6}
- [定義] 以下の定義において,例1を具体的な例として説明を行う.
- 和事象 A∪B: 事象AまたはBが起こるという事象.例えば,事象Aを「4 以下の目が出る」,また,事象Bを「偶数の目が出る」事象としたとき,事象「A∪B」は,{1,
2, 3, 4, 6} となる.
- 積事象 A∩B: 事象AとBが同時に起こるという事象.例えば,事象Aを「4 以下の目が出る」,また,事象Bを「偶数の目が出る」事象としたとき,事象「A∩B」は,{2,
4} となる.
- 余事象 A: 標本空間Ωの中で,事象Aが起こらないという事象.例えば,事象Aを「4
以下の目が出る」事象としたとき,余事象は,{5, 6} となる.
- 排反事象 事象AとBが同時に起こることがない時,記号的には A∩B = φ である時,事象AとBは互いに排反である,または,排反事象であるという.例えば,事象Aを「奇数の目が出る」,また,事象Bを「偶数の目が出る」事象としたとき,これらの事象は排反である.
|
- 2.2 確率の定義
- [定義] 標本空間Ωの各事象Aに対して次の3つの条件を満たす実数 P(A) が対応させられるとき,その値
P(A) を事象Aの起こる確率という.各事象に対して確率が与えられる標本空間を確率空間といい,各事象を確率事象という.
|
- 任意の事象Aに対して,0 ≦ P(A) ≦ 1
- P(Ω) = 1, P(φ) = 0
- 事象AとBが互いに排反,即ち A∩B = φ ならば,以下の関係が成立する.
- P(A∪B) = P(A) + P(B)
- 確率現象を表現するのに,各根元事象に対して,各事象が発生する確率を明記した以下に示すような表がよく使用されます.この表のことを,確率分布表と呼びます.
| 根元事象 |
E1 |
E2 |
・・・・・ |
EN |
全事象Ω |
| 確率 |
p1 |
p2 |
・・・・・ |
pN |
1.0 |
- 例2: 例1において,各目が出る事象に 1/6 という数値を対応させると,上の定義から,明らかにこれは確率と成ります.
- 上の例において,各目が出る確率を 1/6 と設定したことに違和感を感じなかったと思います.経験的に,多数回サイコロを投げれば,各目の出が出た回数を試行回数で割った値が,本来そのサイコロが持っている各目の出る確率に近づいていくこと,そして,その値が
1/6 であることを経験的に知っているからです.このことを保証したのが以下に述べる法則です.
- [大数の法則] ある試行を N 回繰り返し行い,事象Aが起こった回数が n 回であるとき,n
/ N を相対度数という.試行回数 N を十分大きくするとき相対度数 n / N が,ほぼ一定値 p
に近づくならば,p を事象Aの起こる統計的確率(確率)という.このように定義された p が,試行回数 N を大きくしていくと,事象Aの本来持っている確率(先験的確率)に限りなく近づくことが知られており,これを大数の法則という.
- 以下,確率に関する定義や定理をいくつかあげておきます.
- [定理]
- 事象A1,A2,・・・,A1 が排反ならば
- P(A1∪A2∪・・・∪Ar)
- = P(A1) + P(A2) + ・・・ + P(Ar)
- 任意の2つの事象A,Bに対して
- P(A∪B) = P(A) + P(B) - P(A∩B)
- 余事象に対して
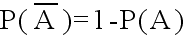
- A⊂Bならば,P(A) ≦ P(B)
|
- [定義] P(A) > 0 であるとき,事象Bに対して,
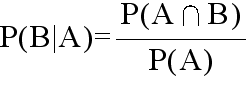
- と定義し,事象Aが起こったときの事象Bの条件付確率という.
|
- [定理] ベイズの定理 事象A1,A2,・・・,Ar が互いに排反であり,かつ,その内どれかの事象が必ず起こるとき,即ち,
- Ai∩Aj = φ ( i ≠ j )
- A1∪A2∪・・・∪Ar = Ω
- ならば,任意の事象Bに対して次の式が成り立つ.
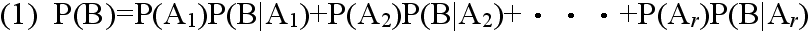
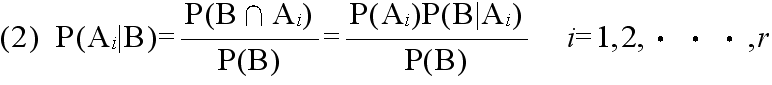
|
- ベイズの定理は,事象A1,A2,・・・,Ar が互いに排反であり,かつ,すべての原因を挙げている場合に,ある事象Bが起こったときそれがどの原因によって発生したかを示す確率
P(Ai|B) を求めるために使用されます.
- 例えば,2つの箱があり,各箱には赤い玉と白い玉が入っていたとします.箱
1 には,赤い玉が 20 個,白い玉が 80 個入っており,また,箱 2 には,赤い玉が
60 個,白い玉が 40 個入っていたとします.今,どちらかの箱から玉を 1 個取り出すものとします.また,各箱から取り出す確率を
P(Ai) ( i = 1, 2 )とします.
- どちらの箱から取り出しても良いとしたとき,各箱から取り出す確率 P(Ai) (事前確率)は,いずれも 0.5 になります.今,どちらかの箱から球を取り出した結果,玉の色は白だったとします.このとき,いずれの箱から玉を取り出したかを示す確率(事後確率)は,
- P(Ai|B) B:白い玉であるという事象
- のように表現でき,取りだした球が白であったという結果によって,事前確率とは異なってきます.具体的に,箱
1 から取り出した確率は,ベイズの定理によって,以下のように計算できます.
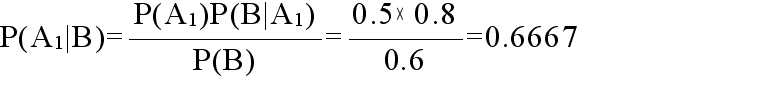
-
- [定義] r 個の事象A1,A2,・・・,Ar に対し,それらの任意個の異なる事象の組合せAi,Aj,・・・,Ak に対して
- P(Ai∩Aj∩・・・∩Ak) = P(Ai) P(Aj) ・・・ P(Ak)
- が成り立つとき,事象A1,A2,・・・,Ar は互いに独立であるという.また,1回毎の試行がそれ以外の試行に何らの影響を及ぼさないとき,すなわち各回の試行が互いに独立であるとき,このような試行を独立試行という.
|
- 3.確率変数
- 3.1 確率変数
- [定義] 標本空間Ωで,ある属性について標本がとる可能性がある異なる数値が
- x1,x2,・・・,xk
- であるとする.各標本に対してそれのとる値を対応させる変数 X を考える.Ω上で
X がそれぞれの値をとる確率が定まっているとき,X を確率変数といい,x1,x2,・・・,xk を X の標識という.
- 確率変数 X が値 xi をとるという事象を
- { X = xi }
- で表し,その確率を
- P(X = xi) = pi (i = 1, 2, ・・・, k)
- で示す.
|
- [定義] 確率変数 X がある値 x に対して,X ≦ x である確率 P(X ≦ x ) を,確率変数
X の確率分布関数という.これを F(x) とすれば,次のようにかける.
- F(x) = P(X ≦ x)
|
- [定理] 確率分布関数の性質
- P(a < x ≦ b) = P(x ≦ b) - P(x ≦ a) = F(b) - F(a)
- x の非減少関数
- 右連続性 limx→a+0F(x) = F(a)
- F(∞) = 1
- F(−∞) = 0
- 0 ≦ F(x) ≦ 1
|
- サイコロを投げるような場合は,確率変数は離散的な値だけを取ることができます.そのような場合を離散型分布といいます.離散型分布に対する確率分布関数は,確率関数( X が xi という値を取る確率に相当),
- fX(xi) = P(X = xi) (i = 1, 2, ・・・)
- を使用して,
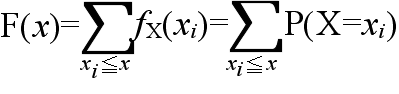
- のように記述できます.例えば,サイコロを投げるような場合における確率関数と確率分布関数は以下のようになります.
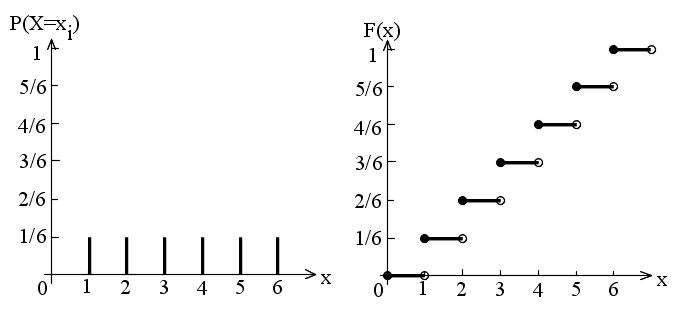
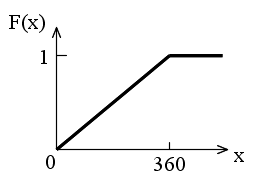
- 確率変数が連続値を取るような分布も存在します.例えば,手で棒を垂直に立てた後,手を離したとします.そのとき,棒が倒れる方向
X は,0 から 360°の間の任意の値を取ることができます.このような分布を連続型分布といいます.棒の例の場合,分布関数の値は角度 x に比例しますので,右図のようになります.
- それでは,連続型分布の場合,離散型分布の確率関数に相当するような関数は存在しないのでしょうか.その答えが下の定義です.
- [定義] 次の式で表される f(x) が存在するとき,f(x) を確率変数 X の確率密度関数という.
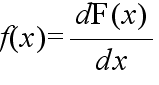
- また,確率分布関数 F(x) は f(x) から
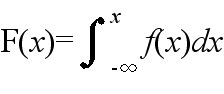
- として与えられる.
|
- 先に述べた棒の例では,その確率密度関数は以下のようになります(右図参照.このような分布を,一様分布といいます).
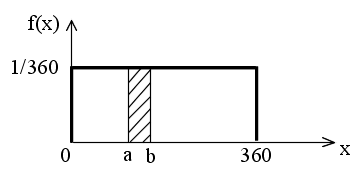
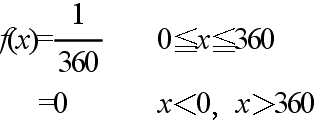
- ここで注意してもらいたいのは,離散型分布の確率関数とは異なり,確率密度関数
f(x) は,X が 値 x を取るときの確率を表しているわけではないことです.この点は,棒の例からも明らかだと思います.例えば,任意の
a ( 0 ≦ a ≦ 360 )の対して,f(a) は 1/360 になりますが,これは決して「倒れたときの角度が
a である確率は 1/360 である」といったことを意味していません.なぜなら,倒れたときの角度がある特定の値に完全に一致する確率は限りなく
0 に近いからです.
- 確率密度関数において,確率としての意味を持つのは上右図の斜線で示した部分の面積です.図の斜線部の面積
S は,下に示すように,倒れたときの角度が a から b の間に入る確率を意味しています.確率分布関数と確率密度関数の関係式において,f(x)dx
を確率( dx を 斜線部の幅 (b - a) とみなす),積分記号を Σ 記号とみなせば,離散型分布との対応が取りやすいかと思います.
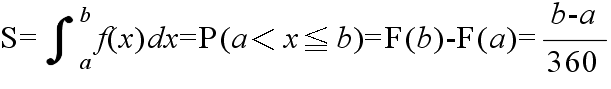
- 3.2 平均と分散
- [定義] 平均(集合平均,期待値)
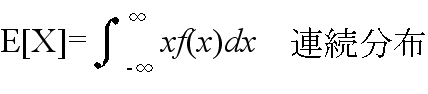
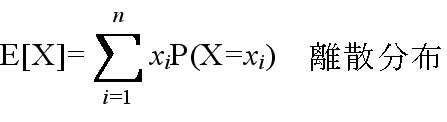
|
- [定義] 分散と標準偏差
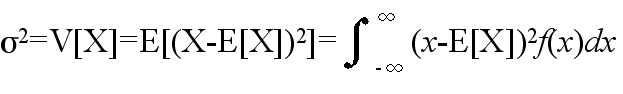
- σ2 を分散,σ を標準偏差と呼ぶ.
|
- [定義] 2つの確率変数 X, Y に対して,以下の式によって定義されるものを共分散と呼ぶ.
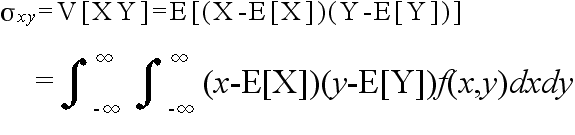
|
- [定理] 平均と分散の性質
- a, b を定数として,E[aX+b] = aE[X] + b
- E[X+Y] = E[X] + E[Y]
- X, Y が互いに独立ならば, E[XY] = E[X]E[Y]
- V[X] = E[X2] - E[X]2
- V[aX+b] = a2V[X]
- X と Y が独立ならば, V[X+Y] = V[X] + V[Y]
|
- 3.3 確率分布
- 確率変数がどのような分布をするかは,先に述べた度数分布表を使って表す場合もありますが,理論的に与えられる確率分布も多くあります.ここでは,代表的な確率分布を紹介します.
- 3.3.1 離散型分布
- 二項分布
- 繰り返し行われる独立試行で,もし各々の試みに対して単に2つの結果だけが可能で,それらが起こる確率が各試行を通じて一定である場合,その試行をベルヌーイ試行といいます.成功の確率が p で失敗の確率が q = 1 - p であるベルヌーイ試行を
n 回行った結果,x 回成功する確率(確率関数)は以下のようになり,この分布を母数
p の二項分布と呼びます.
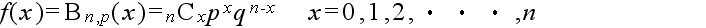
- 二項分布という名称は,この式が,(py + q)n を展開したときの yx の係数に等しいことに由来します.なお,二項分布の確率分布関数,平均,及び,分散は以下のようになります.
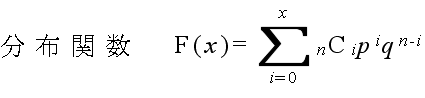
- 平均: E[X] = np, 分散: V[X] = npq
- 二項分布は,n の値が大きくなる( np ≧ 5 と nq ≧ 5 が成立する程度)と後に述べる正規分布,

- に近づきます.
- ポアソン分布
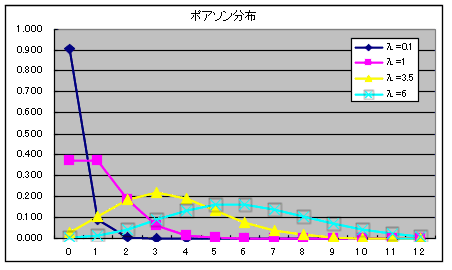 二項分布は,p の値が小さく,n の値が非常に大きくなると,λ = np のポアソン分布に近づきます.単位時間内に到着する電話の呼び数
x の分布等がポアソン分布に従うことが良く知られています.母数 λ のポアソン分布の確率(確率関数),平均値,及び,分散は以下のようになります.
二項分布は,p の値が小さく,n の値が非常に大きくなると,λ = np のポアソン分布に近づきます.単位時間内に到着する電話の呼び数
x の分布等がポアソン分布に従うことが良く知られています.母数 λ のポアソン分布の確率(確率関数),平均値,及び,分散は以下のようになります.
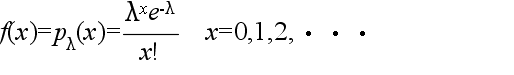
- 平均: E[X] = λ, 分散: V[X] = λ
- ポアソン分布は,λ の値が大きくなる( λ > 10 程度)と,正規分布,

- に近づきます.
- 3.3.2 連続型分布
- 一様分布
- 先に述べた棒の例が一様分布の例です.一様分布の確率密度関数,平均,及び,分散は以下のようになります.
- 密度関数 f(x) = 1 / (b - a) a ≦ x ≦ b
- = 0 x < a, または, x > b
- 平均: E[X] = (a + b) / 2, 分散: V[X] = (a - b)2 / 12
- 指数分布
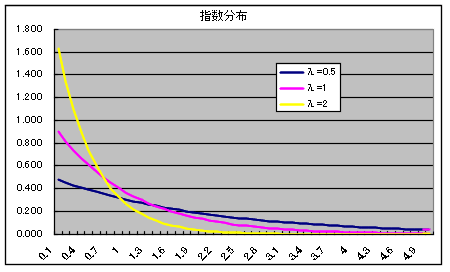
- 指数分布は,ポアソン分布と強い関係があります.例えば,電話の呼び間隔が平均値 1 / λ の指数分布をするとき,単位時間内に到着する電話の呼び数の分布は平均値 λ のポアソン分布をします.母数 λ の指数分布の確率分布関数(右図参照),確率密度関数,平均,及び,分散は以下のようになります.
- 分布関数 F(x) = 1 - e-λx x ≧ 0
- = 0 x < 0
- 密度関数 f(x) = λe-λx x ≧ 0
- = 0 x < 0
- 平均: E[X] = 1 / λ, 分散: V[X] = 1 / λ2
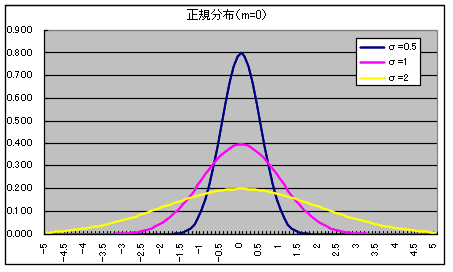
- 正規分布(ガウス分布) N(m, σ2) 密度関数,分布関数,α値の計算

- 正規分布は,非常によく使われる分布です.母数 m,σ の正規分布 N(m,
σ2) の確率密度関数,平均,及び,分散は以下のようになります.
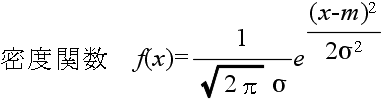
- 平均: E[X] = m, 分散: V[X] = σ2
- 平均値が 0,標準偏差が 1 である正規分布 N(0, 12) を標準正規分布と呼びます.確率変数 X の分布が N(m, σ2) の正規分布に従うとき,次の変数変換(標準化変換)によって得られる確率変数 Z は標準正規分布 N(0, 12) に従います.
- Z = (X - m) / σ
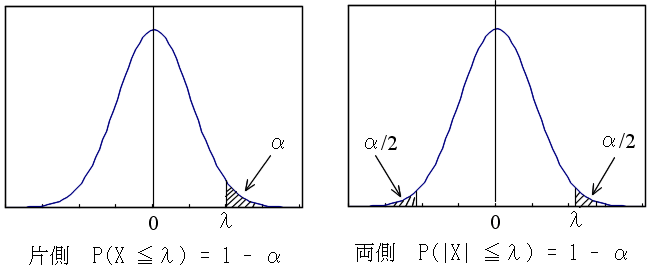
- また,値 α( 0 ≦ α ≦ 1 )に対して,以下の図に示すような値 λ を正規分布の
α 値,または,(α×100) パーセント値といいます.α は,図からも明らかなように,確率変数の値が
λ 以上になる確率(両側の場合は,確率変数の値が λ 以上,又は,ーλ以下になる確率)に相当します.α
点は,後に述べる推定において非常に重要となりますので十分理解しておいてください.なお,以下に述べる各分布に対しても,同様に,α
点を定義することができます.
- 自由度 n の χ2 分布 密度関数,分布関数,α値の計算
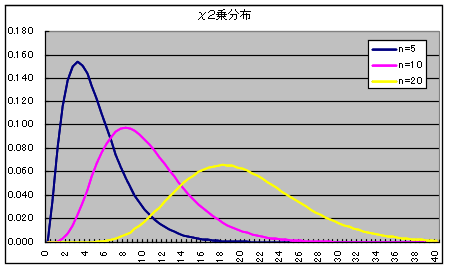
- x1,x2,・・・,xn が互いに独立な確率変数で,それぞれが標準正規分布 N(0, 12) に従うとき,
- χ2 = x12 + x22 + ・・・ + xn2
- なる確率変数 χ2 が従う分布を自由度 n の χ2 分布といいます.自由度 n の χ2 分布の確率密度関数,平均,及び,分散は以下のようになります.
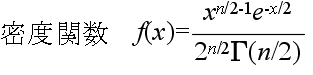
- 平均: E[X] = n, 分散: V[X] = 2n
- ここで,Γ は,ガンマ関数であり,次のように定義されます.(ガンマ関数の計算 )
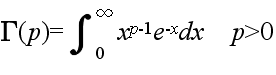
- Γ(1) = 1, Γ(p+1) = pΓ(p)
- Γ(n+1) = n! n: 整数
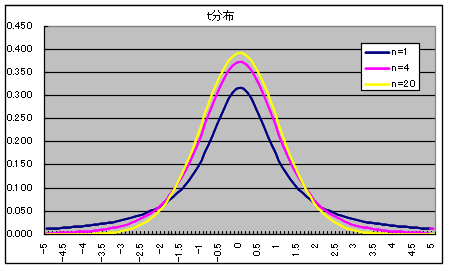
- 自由度 n の t 分布 密度関数,分布関数,α値の計算 →

- x1,x2,・・・,xn が互いに独立な確率変数で,それぞれが標準正規分布 N(0, 12) に従うとき,
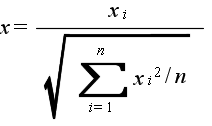
- なる確率変数 x が従う分布を自由度 n の t 分布といいます.自由度 n の t
分布の確率密度関数,平均,及び,分散は以下のようになります.
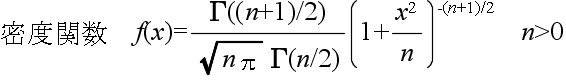
- 平均: E[X] = 0, 分散: V[X] = n / (n - 2) 平均,分散は,n ≧
3
- なお,自由度が大きくなると,t 分布は正規分布に近づき,自由度が無限大になると,標準正規分布
N(0, 12) と一致します.
- 自由度 n1,n2 の F 分布 密度関数,分布関数,α値の計算 →
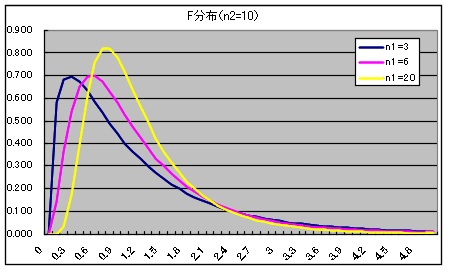
- χ12 が自由度 n1 の χ2 分布,χ22 が自由度 n2 の χ2 分布に従い,かつ,χ12 及び χ22が互いに独立であるとき,
- x = (χ12 / n1) / (χ22 / n2)
- なる確率変数 x が従う分布を自由度 (n1, n2) の F 分布といいます.自由度 (n1, n2) の F 分布の確率密度関数,平均,及び,分散は以下のようになります.ただし,平均に対しては
n2 > 2,分散に対しては n2 > 4 とします.
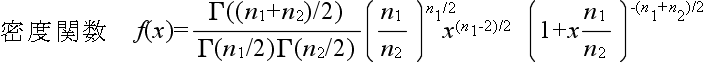

- 4.統計
- 4.1 統計的推定
- 4.1.1 標本と母集団
| [定義] 調査や観測の対象となる属性を持つすべての個体の集合を母集団という.母集団から取り出された一部のデータの集合を標本といい,データの数を標本の大きさという.また,母集団の平均値,分散などを母平均値,母分散といい,一般に母集団の特性値を母数という. |
- 調査や観測等によって,我々が知りたいのは母集団の特性値−母数−です.観測された標本
x1, x2, ・・・, xn から,母数を推定する方法を統計的推定と呼びます.母平均値や母分散を推定する方法として,以下に示すような標本統計量(標本平均値,標本分散などは,母平均値,母分散等に対する点推定値)がよく使用されます.
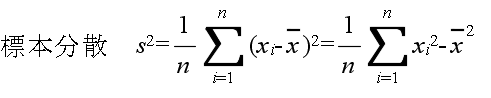

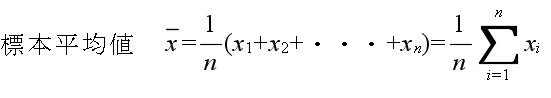
- の統計量の内,分散や標準偏差の概念は多少分かりにくいかもしれません.分散は,データのばらつきを表す指標です.分散が大きいほど,データがばらついていることになります.先に述べた正規分布のグラフを見てもらうと,σ
が小さいほど,尖ったグラフになっています.つまり,σ が小さいほど,データのばらつきが少なく,平均値の周りに集中していることになります.極端な例として,分散が
0 であることは,すべてのデータが同じ値になっていることを意味しています.
- 標本統計量も一つの確率変数です.ある観測で得られた標本平均値や標本分散は,確率変数
X や S2 の一つの実現値であると考えられます.従って,その統計量を計算できます.例えば,標本平均値と標本分散の平均は以下のようになります.
- E[X] = m m:母平均値
- E[S2] = (n - 1) σ2 / n σ2: 母分散
- 上式から明らかなように,標本平均値の平均値は母平均値と一致しますが,標本分散に関しては,一致しません.標本平均値のように,標本平均値の平均値が母平均値と一致するような統計量を不偏推定量と呼びます.母分散の不偏推定量は,以下のようになり,先に述べた標本分散の代わりによく使用されます.

- また,多変数の場合は,以下に示すような標本統計量がしばしば使用されます.
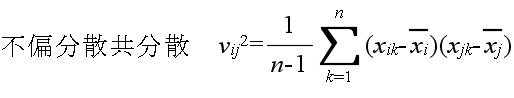
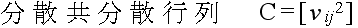
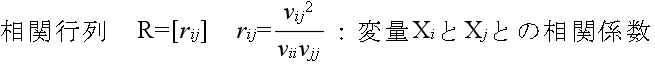
- ただし,
- X1, X2, ・・・, Xm : 確率変数
- xi1, xi2, ・・・, xin : 確率変数 Xi に対する標本
- とします.
- 4.1.2 中心極限定理
| [定理] 中心極限定理 確率変数 X1, X2, ・・・, Xn が互いに独立で,平均値が m,分散が σ2 の同じ分布に従うとき,それらの平均 X の確率分布は,n を十分大きくすれば,正規分布 N(m, σ2/n) で近似される. |
- 中心極限定理が適用できる標本の大きさの目安は,概略,以下の通りです.
- 分布が平均に対して左右対称の場合: n ≧ 30
- 分布が平均に対して左右非対称の場合: n ≧ 50
- 4.1.3 区間推定法
- 先に述べた点推定量には,その値がどの程度信頼できるかの情報が全く含まれていません.そこで,点推定量を元に,母数の値が,どの程度の信頼度で,どの範囲に含まれるかを推定するのが,区間推定です.以下においては,母平均値の区間推定法に関して簡単に述べます.
- 母分散 σ2 が既知の場合
- 母集団が,正規分布 N(m, σ2) に従っているものとします.ただし,標本の大きさ n が大きいときは,必ずしも正規分布である必要はありません.このとき,中心極限定理により,標本平均値
X は,N(m, σ2/n) の正規分布をします.従って,
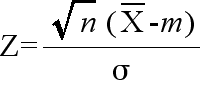
- は,標準正規分布 N(0, 12) をします.A(α) を標準正規分布の α 点とすると,
- P(|Z| ≦ A(α)) = 1 - α
- という関係が成り立ちます.つまり,
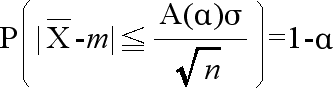
- となります.このことより,推定の信頼度を (1 - α) とすると,母平均の信頼区間は,以下のようになります.
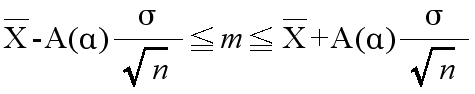
- 母分散 σ2 が未知の場合
- [定理] n 個の確率変数 X1, X2, ・・・, Xn が平均値 m の同じ正規分布に従い,互いに独立ならば,その標本分散を S2 としたとき,
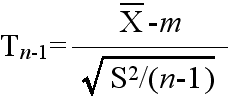
- で定義される確率変数 Tn-1 が,母分散に関係なく,自由度 n-1 の t 分布に従う.
- 上の定理を利用することによって,大きさ n の標本の標本平均値が x,標本分散が s2 であるとき,母平均値 m の信頼度 (1 - α) の信頼区間は,自由度 n-1 の t
分布の α 点を tn-1(α) とすると,以下のようになります.
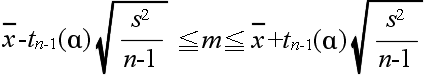
- 4.2 統計的検定
- 4.2.1 仮説検定
- 実験等によって得られた標本統計量に基づき,何らかの推論を行いたい場合があります.例えば,標本平均値からその「母平均値が
m である」ことを検証したい,2つの母集団から得られた標本平均値に基づき,それらの「母平均が等しい」ことを検証したい,といった場合です.このような場合,まず,一つの仮説
H(帰無仮説)をたてます.例えば,上の例では,「母平均値が m である」,「母平均が等しい」などがその仮説に相当します.
- 既に述べたように,標本統計量も一つの確率変数です.同じ母集団から採った標本平均値であっても,常に同じ値になるわけではありません.したがって,2つの母集団から得られた標本平均値が同じ値になったとしても,必ずしも2つの母集団の母平均値が等しいことを意味しているわけではありません.同様に,2つの標本平均値が異なっていても,それらの母平均値が異なっているとは限りません.
- そこで,以下に述べるような方法によって仮説の正誤を判定します.標本統計量は設定した仮定の下で何らかの分布をします.得られた標本統計量がその分布の滅多に起こらないような値であったとします.例えば,標本統計量が平均値
50,標準偏差 10 の正規分布をするとき,実際に得られた標本統計量が 85 であったような場合です.実際,このようなことが起こる確率は,0.001
以下です.このような場合に対する解釈として2つあります.一つは,滅多に起こらないことが起こったという解釈です.他の一つは,設定した仮定が間違っていたという解釈であり,一般には,この解釈を採用します.その際,先に述べた
α 値((α×100) パーセント値) λ を使用します.つまり,得られた統計量の値が
λ より大きいまたは小さいとき(得られた統計量の値が実現する確率が α 以下であるとき),最初の過程が誤っているものとして棄却します.この方法を仮説検定といいます.
- α 値((α×100) パーセント値)として,普通,5 %,または,1 %が用いられ,これを有意水準といいます.仮説Hが有意水準 α で棄却されたとき,検定結果は水準 α で有意差があるといいます.また,仮説を棄却する範囲のことを棄却域といい,確率分布の片側または両側に棄却域をとる場合を,それぞれ片側検定,または,両側検定といいます.
- ある仮説が棄却されたとしも,仮説が誤っていることを意味しているわけではありません.あくまで,得られたデータのもとでは,誤っている可能性が高いことを示唆しているにすぎません.同様に,棄却されなかったとしても,仮説が正しいことを意味しているわけではないことに,十分注意してください.
- 4.2.2 平均値の検定
- 検定目的や条件によって,様々な検定方法が存在しますが,ここでは,平均値の検定について簡単に述べます.詳細については,統計に関する書物等を参照してください.
- [定理]平均値の検定(母分散が既知の場合) 母集団Ωの母平均値 m に対して,その値が
m0 であるという仮説,つまり,次のような帰無仮説をたてる.
- 帰無仮説H: m = m0
- このとき,Ωからの大きさ n の標本平均値 X は,N(m, σ2/n) の正規分布をする.従って,
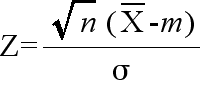
- は,標準正規分布 N(0, 12) をする.そこで,A(α) を正規分布の α 値としたとき,得られた標本平均値
x が不等式,
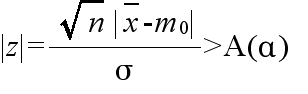
- を満たすならば,有意水準 α で,仮説Hを棄却する.
|
- [定理]平均値の t 検定(母分散が未知の場合) 母集団Ωの母平均値 m に対して,その値が
m0 であるという仮説,つまり,次のような帰無仮説をたてる.
- 帰無仮説H: m = m0
- このとき,Ωからの大きさ n の標本平均値を X,標本分散を S2 としたとき,
.gif)
- で定義される確率変数 Tn-1 が,自由度 n-1 の t 分布に従う.そこで,tn-1(α) を自由度 n-1 の t 分布の α 値としたとき,標本平均値 x と標本分散 s2 が不等式,
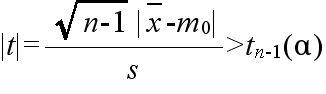
- を満たすならば,有意水準 α で,仮説Hを棄却する.
- 母分散が未知の場合であっても,標本数が大きい場合は,母分散の近似値として標本分散
s2 を用いて,最初の定理を使用することが可能です.
|


























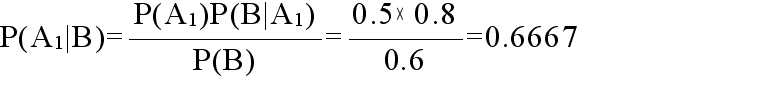
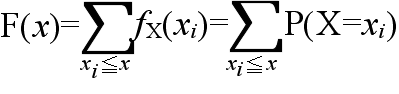
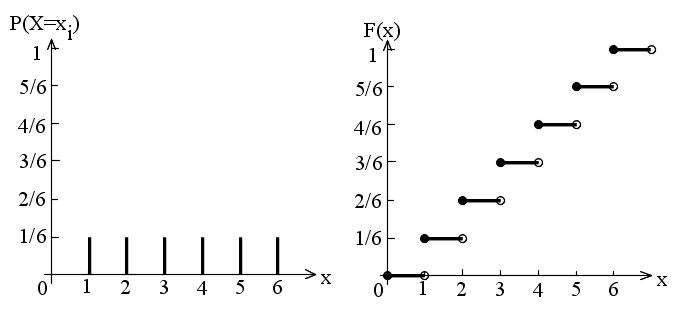


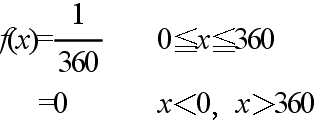
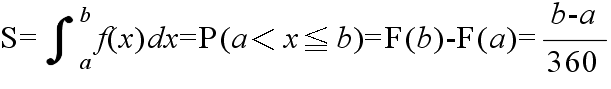

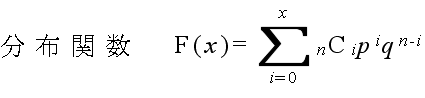
 二項分布は,p の値が小さく,n の値が非常に大きくなると,λ = np のポアソン分布に近づきます.単位時間内に到着する電話の呼び数
x の分布等がポアソン分布に従うことが良く知られています.母数 λ のポアソン分布の確率(確率関数),平均値,及び,分散は以下のようになります.
二項分布は,p の値が小さく,n の値が非常に大きくなると,λ = np のポアソン分布に近づきます.単位時間内に到着する電話の呼び数
x の分布等がポアソン分布に従うことが良く知られています.母数 λ のポアソン分布の確率(確率関数),平均値,及び,分散は以下のようになります.